Michael Lindstrom

Assistant Professor, University of Texas Rio Grande Valley

UTRGV Photo

PhD, Applied Mathematics, University of British Columbia, 2015

School of Mathematical and Statistical Sciences,
University of Texas Rio Grande Valley

Email: M I K E [then there is a dot] L I [ rest of my last name goes here ] [at] [5 Letters of School Initials] [dot] E D U
Phone: 956 665 7063
Office: EMAGC 3.734

my picture

Contents

Hi! My name is Mike. Thanks for visiting my Applied and Industrial Mathematics webpage. I am an applied mathematician and my research encompasses differential equations, asymptotics, numerical analysis, and data science. You can learn more about what I do by navigating through the tabs.

About Me

Academic:

I'm an Assistant Professor in the School of Mathematical and Statistical Sciences at The University of Texas Rio Grande Valley. Before this, I was an Assistant Adjunct Professor for the Program in Computing at the University of California, Los Angeles, where I also held an NSERC Postdoctoral Fellowship. I completed my doctor of philosophy at the University of British Columbia in Vancouver, BC, Canada.

I've always enjoyed applications of math, but I find theory can be useful and beautiful, too. I've worked on a variety of applied projects, with a few currently underway - see the research portion of this page for details of the various projects. To be very brief, the problems I'm currently working on are:

These projects combine many fascinating mathematical fields including ordinary and partial differential equations, data science, asymptotic analysis (analytic approximation schemes), and numerical analysis (studying how the problems can be coded and accurately solved with a computer). At the end of the day, though, being able to say something about the real world is what motivates me most (although the math is super cool!!!).

Personal:

I grew up in Winnipeg, Manitoba—the mosquito capital of Canada... also famous for the fantastically cold winters, which I am pleasantly reminded of each year when I go back to see family and friends over the break.

I completed my university education in the beautiful city of Vancouver, British Columbia (at UBC), with tons of beautiful parks and hiking trails in close proximity. I'll miss Vancouver's stellar public transit system, close proximity to nature, countless delicious restaurants, and amazing simultaneous views of the mountains and ocean!

I did live in Los Angeles for a number of years doing my postdoc at UCLA. While I can't say that LA was my favourite city, I did enjoy the weather. The food was also pretty good, but nothing was accessible without an extensive commute.

I really like the Rio Grande Valley so far: the people are friendly and the cost of living is very reasonable. The weather kills me, though. Being Canadian, I don't deal with heat very well.

Some other interests include:

I'm also a fan of Piled Higher and Deeper comics (reasonably accurate depictions of what it's like to be a grad student—I remember those days...).

Research

Research Experience and Interests

Projects I have worked on / am current work on are below.

Current Work
  1. Air Turbulence: though the 2022 Montreal IPSW, we began a proof of concept for a method to impute turbulence for short intervals in the future based on prior readings local in space and time. We are now working to optimize the method and improve our knowledge of the physics.
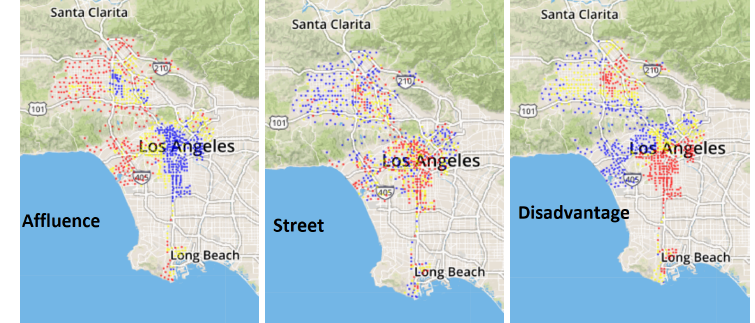
  2. Homelessness: Los Angeles, along with many major cities, has a huge homeless problem. Right now there are over 50,000 homeless people in Los Angeles, and the problem is very complicated. There is little understanding as to the mechanisms that yield such high rates of homelessness and how individual characteristic traits influence the outcome of homeless individuals. Read More. topic model of homeless populations
Past Work
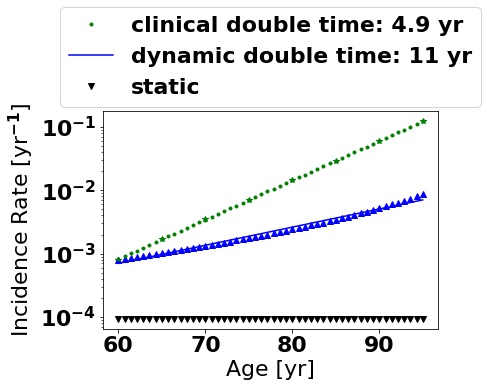
  1. Alzheimer's Disease: Alzheimer's Disease is a tragic disease resulting in the gradual loss of memory and cognitive function and currently the most common dementing illness in the world with incidence (one's risk) doubling every 5 years! Read More. risk vs age for AD
  2. COVID-19: the global pandemic of COVID-19 has brought many challenges in how we deal with it as a society to keep everyone safe, to predict future outcomes, and to understand disease mechanisms. I'm working wrapping up a few projects related to this disease— and maybe more will start up.
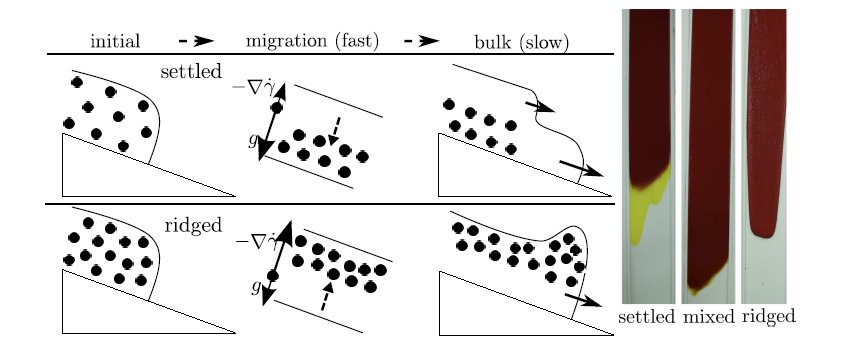
  3. Fluid Flows: When particles are suspended in a highly viscous oil and allowed to flow down an incline, there are two qualitatively distinct regimes: at low particle concentration / inclination angle, the fluid and particles separate; at high particle concentration / inclination angle, the particles stay mixed in the fluid and become more concentrated at the leading front. In some experiments we ran, we noticed the particles and fluid stayed well mixed and didn't bifurcate over the length of the incline. Read More.physical mechanisms and results of shear induced migration
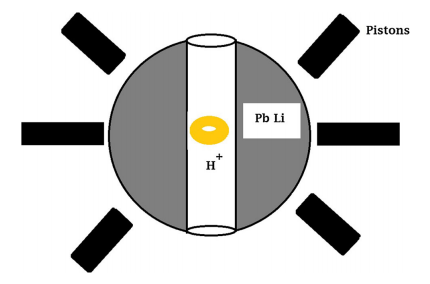
  4. Nuclear Fusion: Magnetized target fusion is a relatively new idea for producing conditions for hydrogen fusion on earth. The essence of the idea is to confine a plasma in a magnetic field and compress it by an intense pressure-focused pulse so that it yields a high enough particle density and pressure for fusion to take place, releasing energy. Read More.sketch of magnetized target fusion reactor
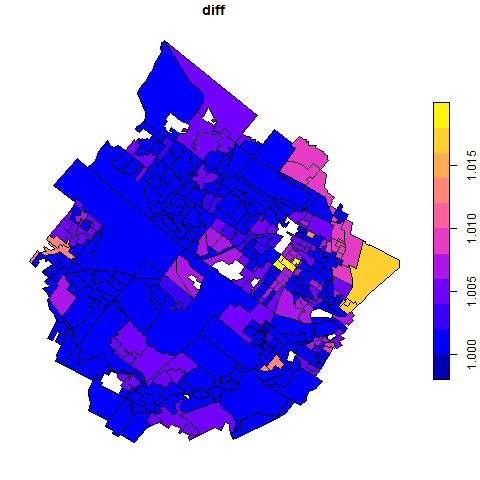
  5. Spatial Risk Segmentation: Through an industrial problem solving workshop in Montréal, a team of us worked to develop and adapt interpolation methods to predict the risk a client will need to make a claim on property insurance using geographic features and client-specific information. We used Geographically Weighted Regression, Poisson Kriging, and Fused Lasso to estimate how risk varies over space. spatial arrangement of risk map
  6. Twitter Data: Twitter is a popular social network where users "tweet" short stories, comments, or ideas. The tweets themselves have a well-defined time, but also may include geotagging information such as the location the tweet was made. The amount of things one can do with this data is almost unlimited. We have focused upon dynamically clustering the tweets into topics and using the topics and information within the text of a tweet to infer a user's location information. We also found it is possible to predict the time/location of a "current event" by studying the frequency of tweets over space and time along with their corresponding topics.
  7. Osteogenesis Imperfecta VI: OI type 6 is a severe form of brittle bone disease where patients have bones that are both very soft (due to delayed mineralization) and very brittle (due to over mineralization). Researchers of the disease suspect an abnormally low concentration of a protein known as PEDF is responsible for the disease. Through an industrial workshop in Montréal, a group of us began to study the process of bone mineralization and the potential role of PEDF with mathematical models. Our work is very preliminary, but our current model qualitatively predicts the delayed bone development of OI type 6 patients if these patients have a decreased concentration threshold of calcification-inhibiting enzymes necessary for bone development. Here are slides from our oral report.
  8. Superconductors: a superconductor, when in the Meissner state, expels magnetic fields from its interior. Very near its surface, there is an exponential decay in field strength that is predicted by the London equation, a special limit of the Ginzburg-Landau equations, provided the surface is flat. In the superconductivity literature, the assumption of a flat interface was taken for granted, but due to experimental measurements of a non-exponential decay in field strength near the surface of a superconductor, experimentalists asked the question of whether small-amplitude perturbations could have an effect on the field profile. Read More. AFM image of superconductor surface
  9. Electrodialysis: Some modern plans for water filtration systems that purify salt water and those that can reduce the waste water of fracking use electrodialysis as a means to pass ions through selectively permeable membranes with the help of an electric potential gradient. I was involved in simulating the system under various settings, employing a combination of asymptotics and numerics. A paper that combines the theoretical work with experiment is here.
  10. Mass Spectrometry: A mass spectrometer separates atoms and molecules based on their mass. This has applications in detecting heavy metal or radioactive contaminants in air or water supplies. At a recent problem solving workshop, a group of us worked in collaboration with PerkinElmer on creating a new method of mass spectrometry that allows for continuous measurements of concentrations, without the costly use of magnetic fields. We found that it may be possible to create an electric field configuration that causes periodic oscillations dependent upon mass, which would allow for different chemical species to be separated spatially or detected with Fourier analysis. Our article on the problem is found here.
  11. Gas Diffusion in Fuel Cells: Fuel cells are costly to build, and developing accurate techniques to simulate their performance beforehand is essential in minimizing production costs. Unfortunately, there are many complex processes that take place within a fuel cell, one of the most important processes is gas diffusion. Those in industry who work with numerical simulations are often puzzled as to what formulation to adopt for gas diffusion: Fick (a simple gradient flow often formulated with a single Fick diffusion coefficient) or Maxwell-Stefan (a complex flow rate that depends upon the concentration gradients of all other species and experimentally determined binary diffusivities). The research I have been involved with on this topic was in studying the two formulations in a simple one-dimensional model of a PEMFC gas diffusion layer. Through nondimenzionalization, and a two-term formal asymptotic expansion, the two models provide nearly identical predictions. Furthermore, Fick diffusion is really a special limit of Maxwell-Stefan diffusion and in many industrial applications, the simpler Fick formulation can be used with reasonable precision. A paper explaining these results has been submitted to Heat and Mass Transfer.
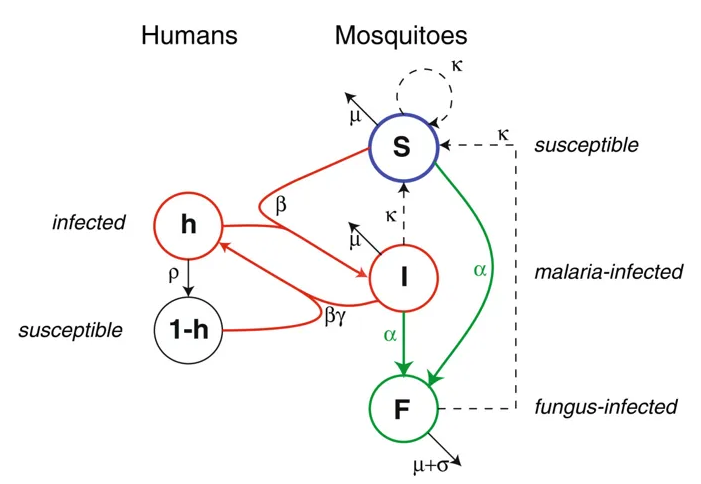
  12. Malaria Management: Recently, a fungus has been discovered that could help reduce malaria-prevalence in endemic regions. The fungus infects mosquitoes, but instead of killing them like a pesticide, it kills the malaria that they carry and could transmit to humans. One biological question that arises is, if this fungus is used, should it be engineered to also kill mosquitoes? Read More.compartment model of malaria with fungus present
  13. Homicide: within homicide cases, there are many levels of detail that are poorly understood scientifically, including temporal patterns of homicide, how they relate to background levels of violence, whether a given case is likely to be closed, etc. Over the 2019 summer, I worked with a team to study these details of homicides and hopefully uncover meaningful insights.
  14. Gang Reduction and Youth Development (GRYD): The GRYD program schedules after-school programs and other supportive interventions for youths who are deemed at risk for joining gangs. We were provided with surveys the participants take, roughly every 6 months, with the surveys asking questions that attempt to measure the participant's attitudes and inclinations towards risky behaviours such as violence or lack of family contact. By modelling the responses as a dynamical system and using Dynamic Mode Decomposition (DMD), we have been able to analyze modes of growth and periodicity within the responses. DMD has also given us a means of predicting future risk-levels with comparable performance to a shallow neural network.

Research Group and Teams

Over the years I have worked with groups of students on research projects. The students have done amazing work and these collaborative projects have been among the most enjoyable experiences I've had in academia.

Through NSF Funding, I am currently recruiting one PhD student (beginning Summer 2024), one-two undergraduate students (beginning Autumn 2023), and a postdoc (beginning Autumn 2024) to join my group.

My current research group consists of

Here are a collection of photos of various research groups and teams I have worked with over the years: so many great memories!

Teaching

Teaching Positions

I am currently teaching courses at UTRGV. Prior to this, I taught at UCLA and at UBC.

The courses I teach and have taught are listed below:

Current:
Past:

Letters of Recommendation:

I feel I should include a short word on writing letters of recommendation. Some things to keep in mind if you ask me to write a letter:

REU Matlab Demo

For a few summer Applied Math REU's, I've taught a crash coursee in MATLAB. Here are some files to demo some of the basic functions/features.

Other Education Stuff

Math Education Resources wiki

I was contributor and administrator for the Math Education Resources wiki. This project began as an online database of past UBC Math Exams with hints and solutions, and has steadily expanded to a more complete online learning resource with questions by topic and interactive features. Currently we're doing an education study on the effectiveness of the wiki.

Papers, Proceedings, Theses, etc.

Journal Papers

Accepted/Published
Preprints/Submissions
  • Miller, E.M., Chan, T.C.D., Montes-Matamoros, C., Sharif, O., Pujo-Mejouet, L., and Lindstrom, M.R., "Oscillations in neuronal activity: a neuron-centered spatiotemporal model of the Unfolded Protein Response" (under revision)

Peer Reviewed Conference Papers:

Non Peer Reviewed Proceedings and Whitepapers:

Theses:

Talks, Posters, Conferences, and Workshops

Upcoming:

Past:

Curriculum Vitae

You can read my CV here (Apr 2023).